Given an undirected graph with nodes labelled from \(1\) to \(N\), list out the adjacent nodes for every node in the graph.

Two nodes are considered to be adjacent if there is an edge connecting the respective nodes.

Input Specification

The first line of the input will contain two integers \(N\) and \(M\) \((1 \le N, M \le 10^5)\), indicating the number of nodes and edges.

The next \(M\) lines will each contain two integers \(a_i\) and \(b_i\) \((1 \le a_i, b_i \le N)\), representing a bidirectional edge connecting the nodes \(a_i\) and \(b_i\).

For this problem you may assume that there exists at most \(1\) edge between any two nodes.

Output Specification

Output \(N\) lines, with the \(i\)-th line representing the adjacent nodes of node \(i\). The nodes are \(1\)-indexed and should be printed in increasing order for each line. For this problem you may assume that there is at least one neighbor for every node.

Sample Input 1

5 7
2 1
1 3
2 2
3 4
2 3
5 3
5 4

Sample Output 1

2 3
1 2 3
1 2 4 5
3 5
3 4

Sample Explanation 1

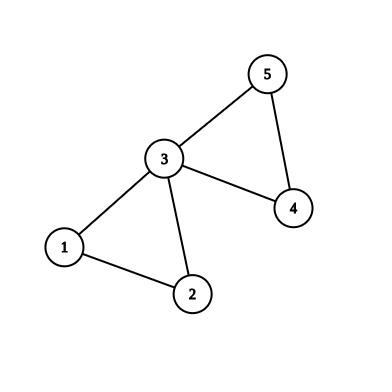
The following image shows the graph found in the sample input. Note that node \(2\) has an edge connecting to itself.