Not only did Bob fail both math and physics, he is taking Ls everywhere else as well!

In fact, Bob is taking so many Ls he is starting to see Ls everywhere! Looking at the \(N\) visible stars in the night sky the Ls are everywhere! But exactly how many are there? As Bob's friend, please help him end this misery!

The \(N\) stars are represented as \(N\) integer coordinates in the Cartesian plane. An \(L\) is defined as \(3\) points connected with a right angle. Two Ls are different if at least one of the points used is different.

For this problem, Python users are recommended to use PyPy over CPython.

Input Specification

The first line of the input will contain an integer \(N\) \((1 \le N \le 10^3)\), indicating the number of stars in the sky. The stars will all have a distinct coordinate.

The next \(N\) lines of the input will contain \(2\) integers ranging from \(-10^9\) to \(10^9\) inclusive, indicating the coordinate of the \(i\)-th star in the Cartesian plane.

Output Specification

Output an integer, representing the number of Ls in the sky.

Subtasks

Subtask 1 [40%]

\(1 \le N \le 50\)

Subtask 2 [60%]

No additional constraints.

Sample Input

5
0 0
-3 0
-2 3
0 5
3 2

Sample Output

3

Sample Explanation

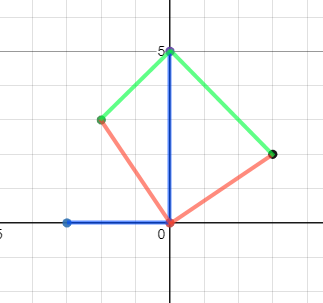
The three Ls are illustrated in red, green, and blue in the following image: