Finding the point of intersection between two functions is a very useful function found in graphing calculators.

You are given two polynomial functions. Given a range \([L, R]\) find the point of intersection. A point of intersection is defined as the location in the Cartesian plane where the two functions cross each other. The given range will always contain exactly one point of intersection that is not located at the exact endpoint of the range.

Input Specification

The first line of input will contain four integers \(N\), \(M\), \(L\), and \(R\) \((1 \le N, M \le 8, -100 \le L \le R \le 100)\), representing the number of terms in the two polynomial functions and the range of query.

The second line of input will contain \(N\) integers. The \(i\)-th number represents the coefficient of the term with degree \(i\) (the first term has a degree of \(0\)). The coefficients will range from \(-10\) to \(10\) inclusive.

The last line will contain \(M\) integers representing the coefficients of the second polynomial function.

Output Specification

Output two decimal numbers representing the point of intersection. Your answer will be considered to be valid if the relative error is within \(10^{-5}\) of the expected solution.

Sample Input 1

3 2 5 10
-1 -4 1
0 2

Sample Output 1

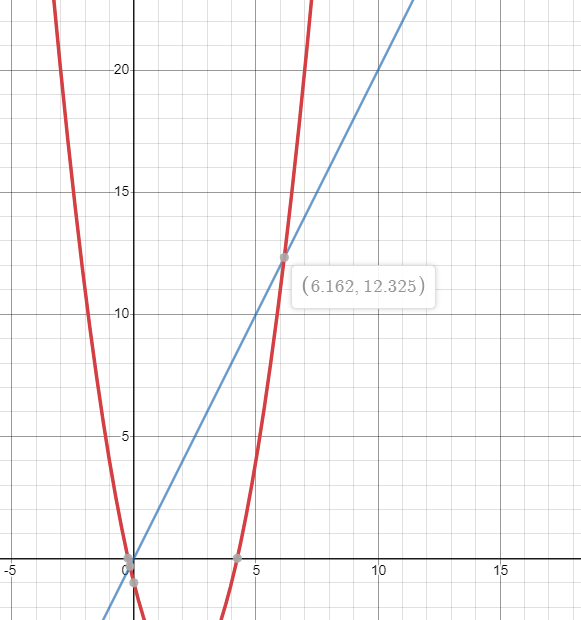
6.16227766 12.32455532

Sample Explanation 1

The first function is represented as \(x^2 - 4x - 1\). The second function is represented as \(2x\). The following image shows the point of intersection: